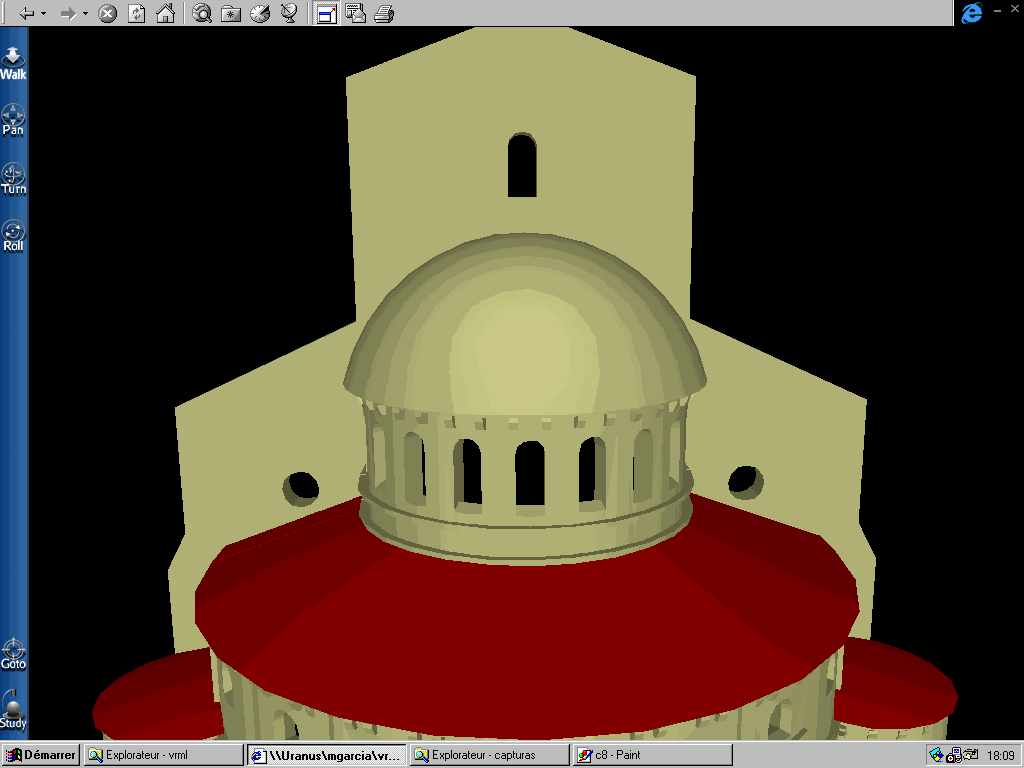
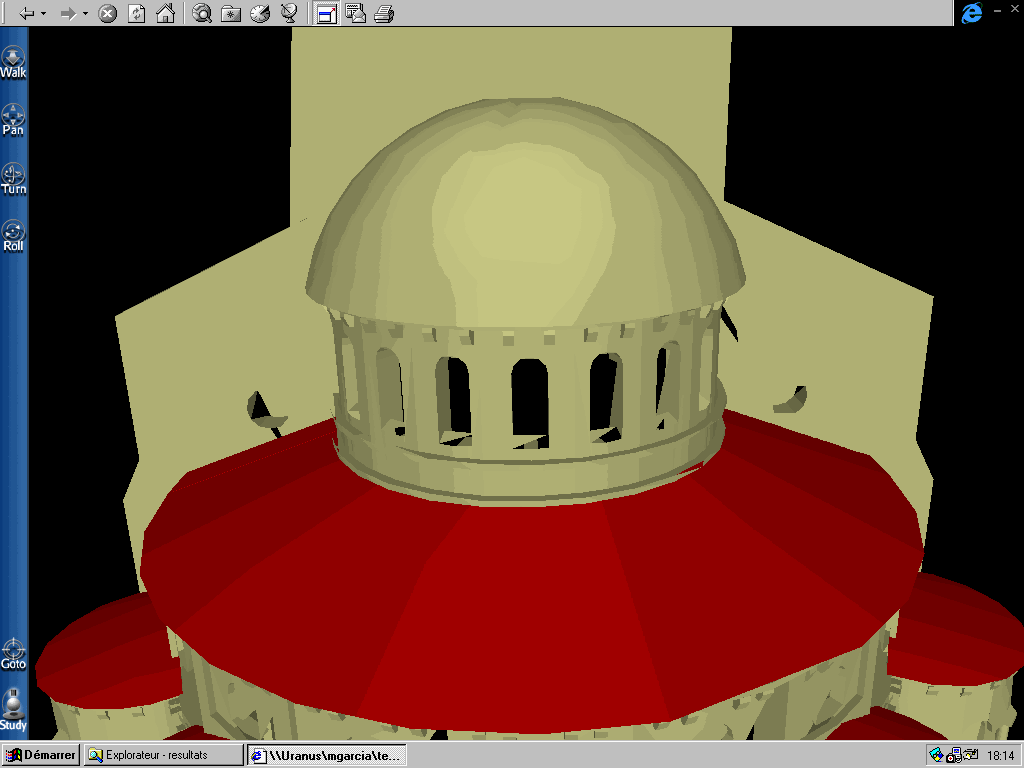
Cluny.wrl : modèle original Clunys20.wrl : modèle décimé
Figure 18 : Détail de la coupole de l?abbaye avant et après la décimation
Évaluation des Résultats
Le prototype a été évalué avec le fichier de l'abbaye de Cluny. Ce fichier a subi plusieurs degrés de décimation pour apprécier les résultats de l'application de l'algorithme de décimation.
Le tableau 1 montre les résultats obtenus par le prototype lors de plusieurs décimations du fichier modèle (Cluny.wrl). En modifiant le pas de décimation, c'est-à- dire la périodicité (en nombre de polygones) avec laquelle le prototype réalise l'opération de l'" edge-collapse ", on obtient différents degrés de réduction.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 1 : Résultats de la décimation.
Si on regarde de près les effets de la décimation on peut observer qu'effectivement, l'algorithme réalise la décimation attendue. Sur le détail de la coupole du modèle de l'abbaye de Cluny (Figure 18), on remarque le résultat de l'application de l'" edge-collapse " sur une configuration de huit polygones.


Cluny.wrl : modèle original
Clunys20.wrl : modèle décimé
Figure 18 : Détail de la coupole de l?abbaye avant
et après la décimation
Cependant, le lissage réalisé par le visualiseur tridimensionnel masque le travail du prototype. Il s'agit du résultat visuel demandé puisqu'on cherche à maintenir la fidélité au modèle tout en réduisant le nombre de polygones formant la maille. Or pour évaluer les résultats de la décimation il faut faire une étude de la structure de la maille polygonale du fichier décimé.
La figure 19 nous montre la maille polygonale originale du fichier Cluny.wrl. Elle subit l' " edge-collapse " suivant le pas de décimation donné.
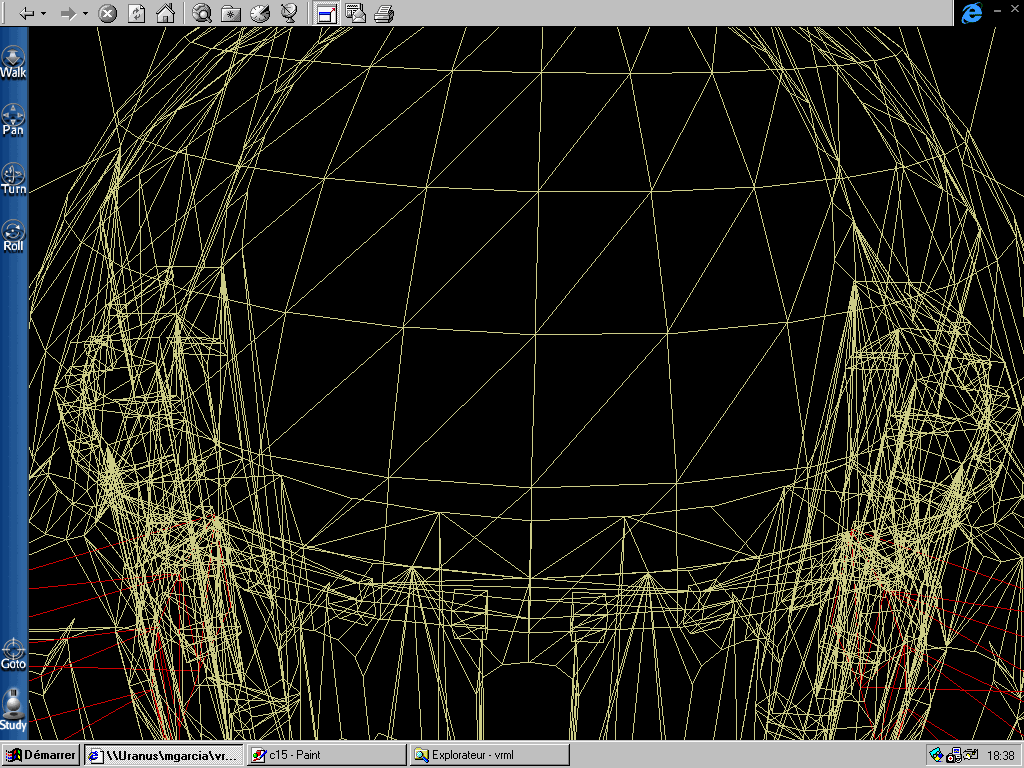
Figure 19 : Détail filaire de la coupole de l'abbaye
avant la décimation
La figure 20 nous montre comment s'est opéré
la méthode de décimation sur la configuration polygonale
au centre de l'image. Dans la maille originale (figure 19),
il s'agissait d'une configuration formée par huit triangles, après
la décimation effectuée (avec un pas de 20 triangles) on
peut observer que la configuration est réduite à une formation
de six triangles sans perte visuelle de résolution (figure
18).

Figure 20 : Détail filaire de la coupole de l?abbaye
après la décimation.
Désormais, l'algorithme ne se comporte pas de façon idéale.
Lorsque la méthode d'élimination d'arêtes, s'effectue
sur le bord d'un objet, elle provoque une déformation du modèle.
Sur la figure 21 on peut voir la déformation
que subit la maille polygonale quand l'" edge-collapse " se produit sur
le bord. Lorsque le point V1 fusionne sur V2, le contour de l'objet est
altéré.
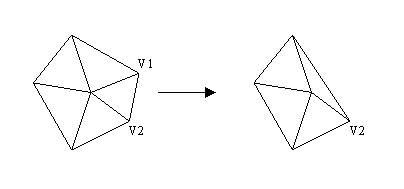
Figure 21 : Déformation. " Edge collapse ", V1
fusionne sur V2
Le prototype va donc provoquer une déformation des objets décimés chaque fois qu'il appliquera la méthode de l'" edge collapse " sur n'importe quelle arête située sur un des bords de l'objet.
Sur la figure 22 on apprécie clairement les
déformations qui se produisent sur les bords du modèle de
l'abbaye de Cluny.
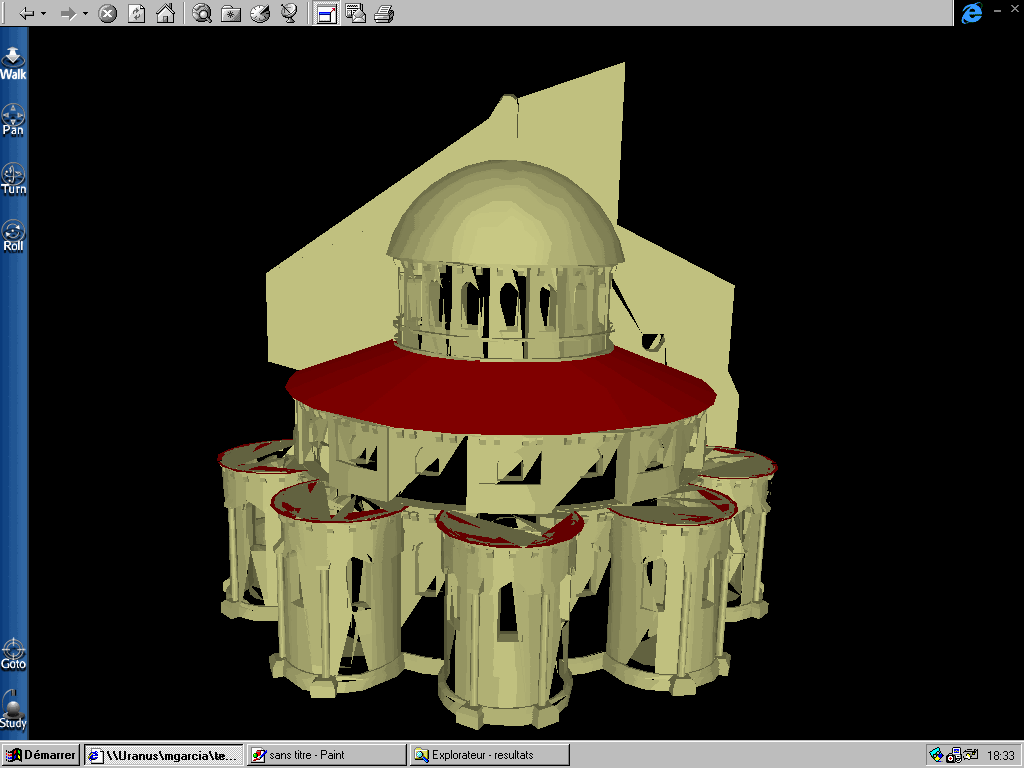
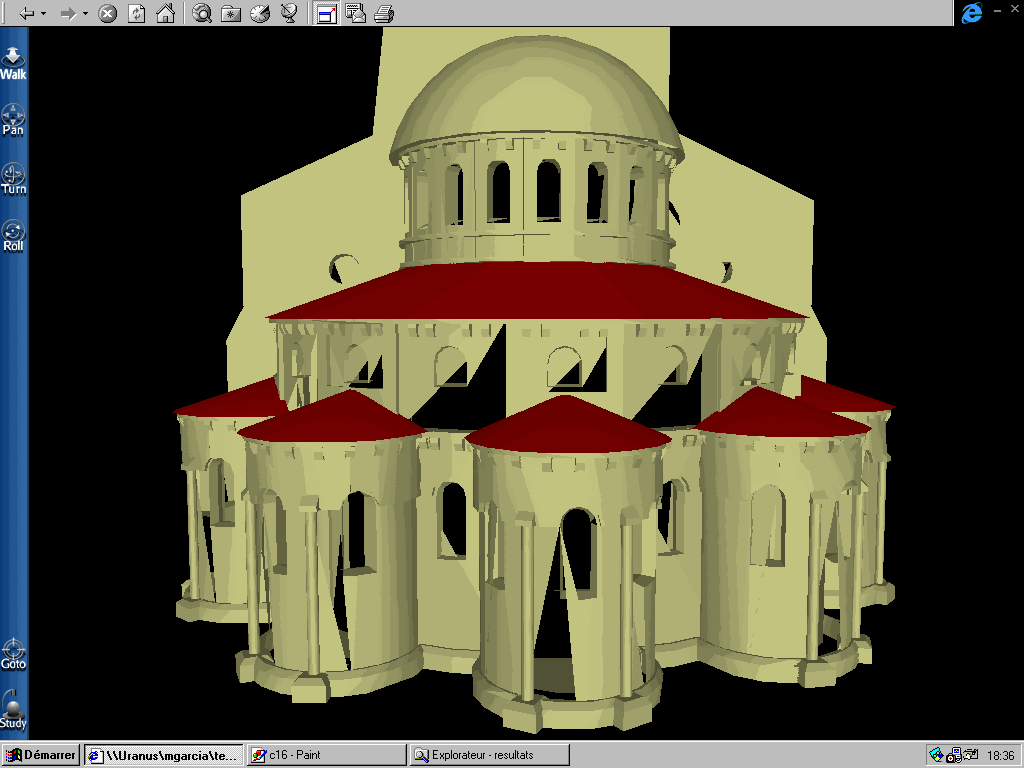
PAS = 20
PAS = 10
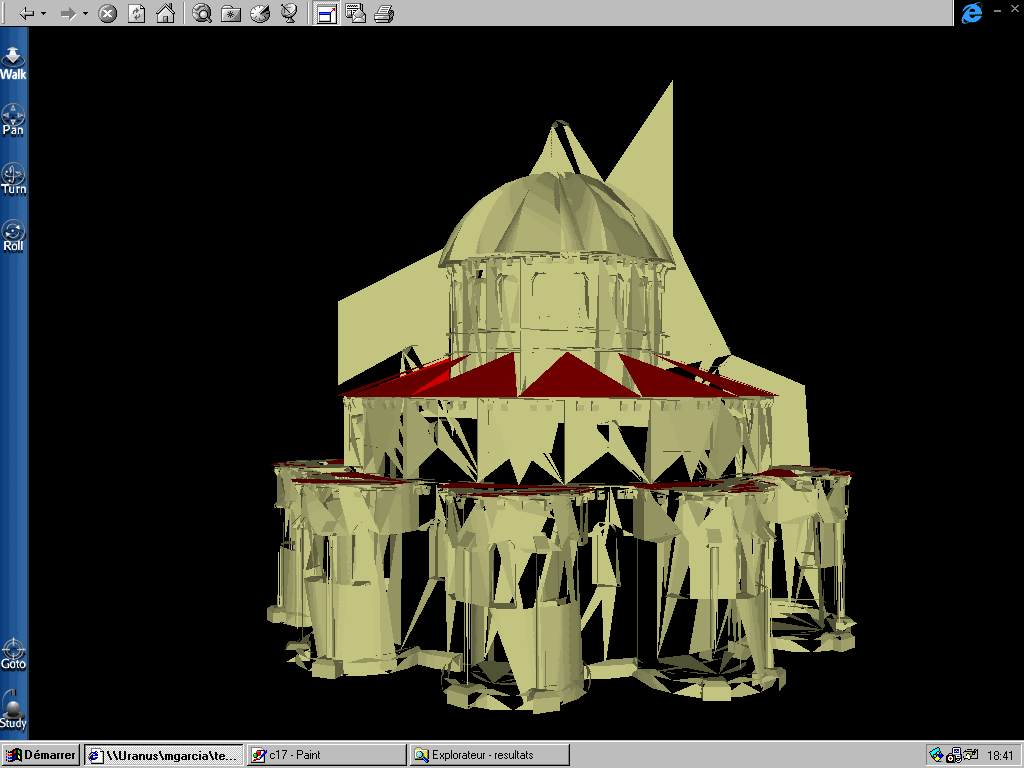
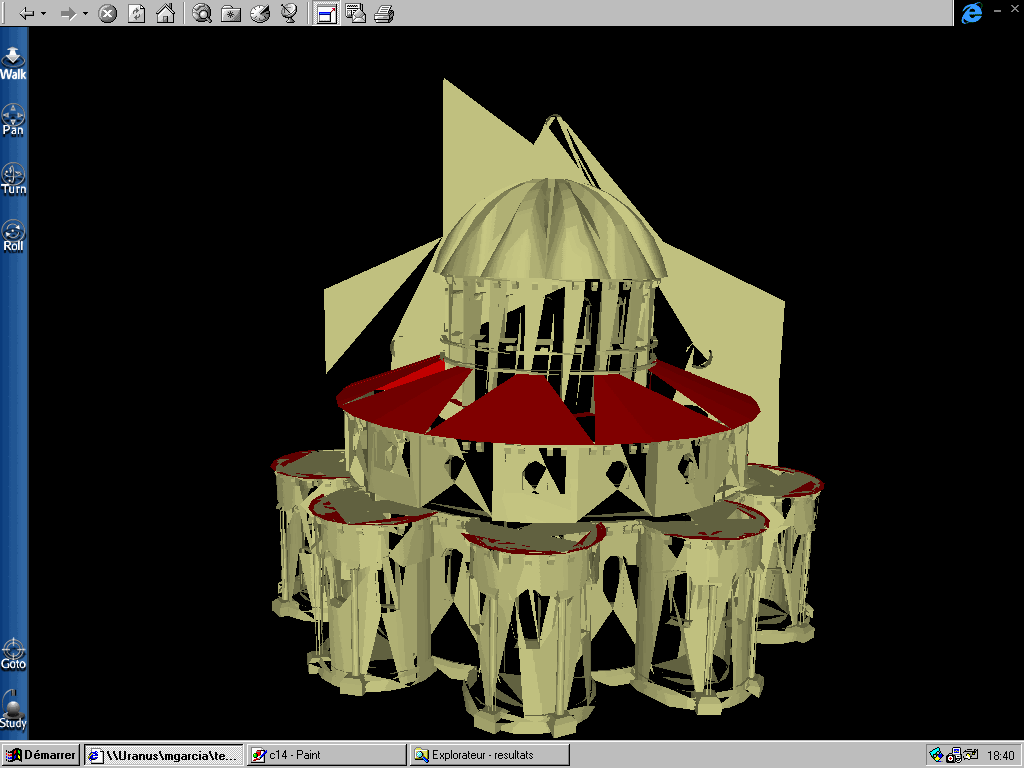
PAS = 5
PAS = 3
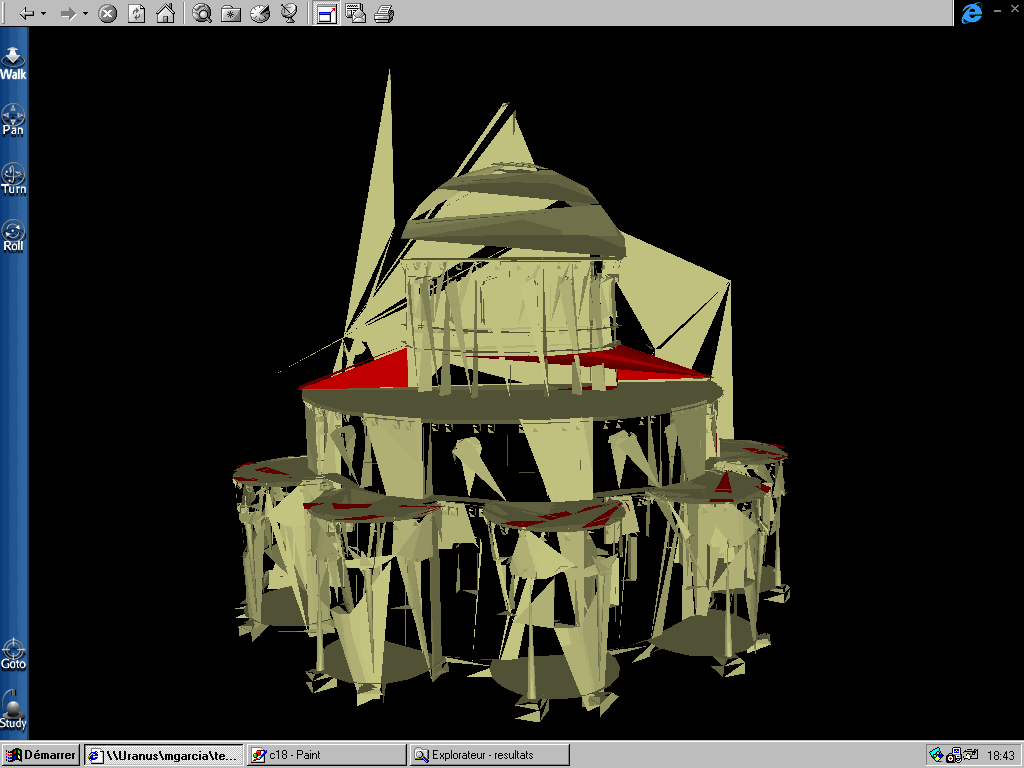

PAS = 2
Détail de la coupole PAS = 2
Figure 22 : Déformations successives pour différents
pas de décimation
Plus le pas de décimation est petit, plus de fois l'algorithme
met en oeuvre la méthode de l'" edge-collapse ". Par conséquent
la probabilité de supprimer une arête appartenant à
un bord augmente avec le taux de décimation.