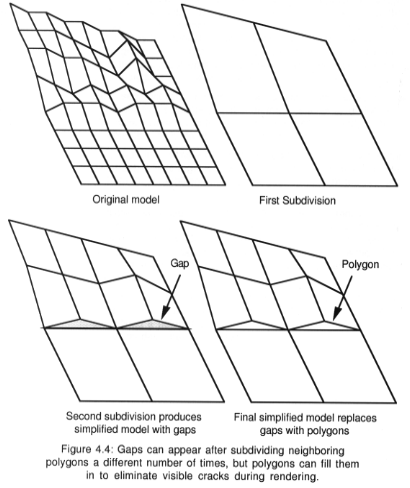
Figure 5 : Subdivisions successives: apparition et remplissage des trous.
La Décimation
L'objectif de mon projet est centré sur le traitement des noeuds
IndexedFaceSet
pour réduire le nombre de polygones composant ces macrostructures.
Il sera donc nécessaire d'aboutir à une simplification polygonale
tout en respectant la topologie générale du monde et en conformité
avec la norme géométrique choisie : le VRML.
3.1 État de l'art des méthodes de simplification polygonales
La simplification polygonale va non seulement augmenter la vitesse de
rendu des scènes, mais aussi réduire la taille des fichiers.
Cela permettra la transmission et le téléchargement des fichiers
sur les réseaux, notamment Internet, et augmentera l'efficacité
et la fluidité lors de la navigation dans les mondes virtuels générés
par ces modèles polygonaux.
3.1.1 Classification des algorithmes de simplification
Les algorithmes de simplification peuvent être regroupés [Erikson 1996] en trois grands ensembles :
3.1.2 Algorithmes préservant
la topologie
3.1.2.1 Simplification des objets rendus par des approximations polygonales
Cet algorithme [DeHaemer & Zyda 1991] utilise la technique de subdivision adaptative et suppose que le modèle original est issu d'un scanner tridimensionnel (Height Field Model), c'est-à-dire que pour chaque point appartenant à une grille rectangulaire régulière, on connaît sa hauteur par rapport à la grille. Cette méthode (Figure 5) utilise la disposition régulière des données, c'est pourquoi elle ne simplifie pas arbitrairement les modèles tridimensionnels.
L'algorithme commence par considérer le modèle comme un
seul polygone puis calcule l'erreur par rapport au modèle source
(en termes de distance). Si l'erreur est plus grande que celle spécifiée
par l'utilisateur, l'algorithme subdivise le modèle simplifié
puis recalcule l'erreur. Le processus s'arrête quand l'erreur se
trouve au dessous des spécifications de l'utilisateur.

Figure 5 : Subdivisions successives: apparition et remplissage
des trous.
Cet algorithme est utilisé pour les modèles de représentation
topographique: height fields models.
3.1.2.2 Optimisation géométrique
Cet algorithme [Hinker & Hansen 1993] de suppression
géométrique (Figure 6) élimine plusieurs
polygones coplanaires et les remplace par un nombre de polygones inférieur.
Cependant, dans le cas de modèles présentant une courbure
considérable, on trouve difficilement de grandes régions
avec des polygones suffisamment coplanaires, c'est-à-dire, qui puissent
être considérés comme appartenant au même plan
(on permet une erreur donnée, et qui peut être définie
comme la distance maximale du polygone au plan ).
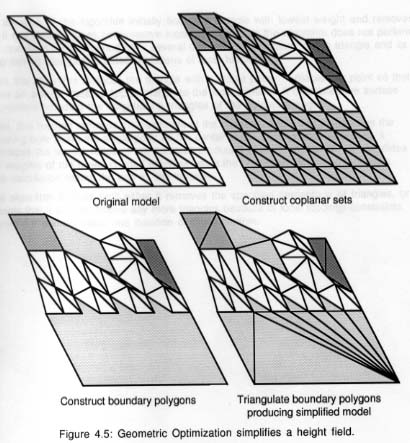
Figure 6 : Simplification d'un Height Model par
optimisation géométrique.
3.1.2.3 Schéma de réduction des données pour les surfaces triangularisées
Cet algorithme [Hamann 1994] de suppression géométrique
applique un poids particulier à chaque triangle du modèle
original en fonction de sa courbure. La simplification (Figure
7) s'effectue rarement sur les régions à grande courbure
et par contre elle se produit souvent dans les régions à
faible courbure. Ainsi l'algorithme simplifie automatiquement les groupes
de polygones coplanaires. L'utilisateur spécifie un pourcentage
de triangles à éliminer du modèle et la simplification
continue jusqu'à ce que le pourcentage demandé soit atteint.
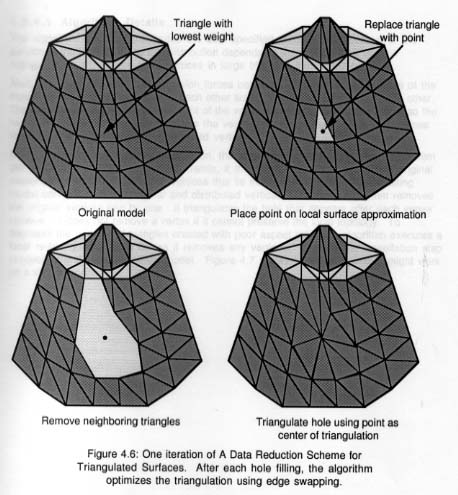
Figure 7 : Itération de l'algorithme de réduction
de données pour surfaces triangularisées
3.1.2.4 Retriangularisation des surfaces polygonales
L'algorithme [Turk 1992] commence avec une disposition
au hasard de points sur la surface de l'objet (Figure 8).
Puis, il simule des forces de répulsion entre les points de façon
à obtenir une distribution la plus uniforme possible. Ensuite, l'algorithme
retriangularise la maille en considérant les nouveaux points. Finalement,
il élimine un par un les points correspondant au modèle original.
Cet algorithme d'échantillonnage et de suppression géométrique
obtient des meilleurs résultats sur des modèles qui représentent
des surfaces courbes que sur des modèles présentant des discontinuités
anguleuses (i.e. il fournira une bien meilleure simplification d'un lapin
de GANIL que d'une maison à colombages). L'utilisateur doit déterminer
le nombre de sommets du modèle recherché.
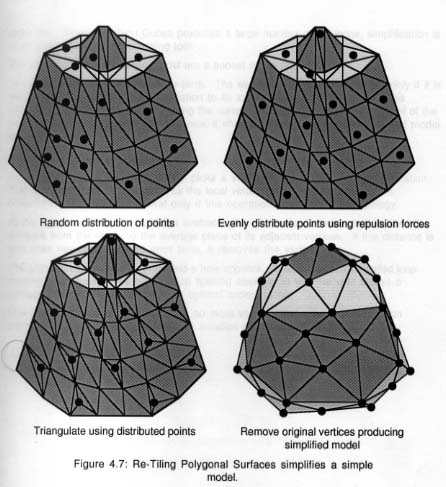
Figure 8 : Retriangularisation de surfaces polygonales
3.1.2.5 Décimation de mailles triangulaires
Dans l'algorithme [Schroeder et al. 1992] de
suppression géométrique (Figure 9) : les
sommets résultants de la simplification forment un sous-ensemble
des sommets qui constituent le modèle original. L'utilisateur spécifie
une distance d'erreur qui est utilisée par l'algorithme pour évaluer
s'il peut éliminer un sommet en comparant cette distance avec la
distance de l'approximation au modèle original.
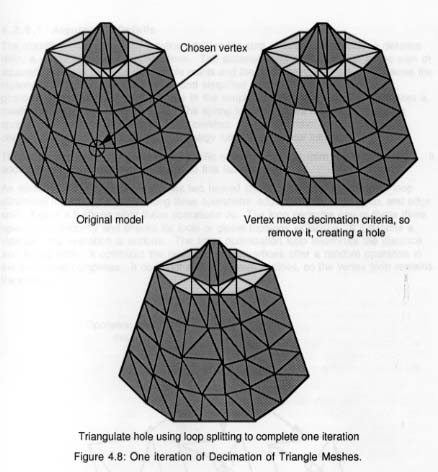
Figure 9 : Itération de l?algorithme de décimation
de mailles triangulaires
3.1.2.6 Optimisation de maille
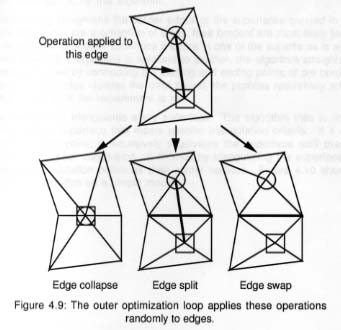
À partir d'une collection de points, un algorithme de reconstruction de surface [Hoppe et al. 1992] génère une maille tridimensionnelle. L'algorithme [Hoppe et al. 1993] simplifie le modèle (Figure 6) en minimisant une certaine fonction appelée fonction d'énergie. Cette fonction tient compte de tous les paramètres géométriques du modèle. Cette minimisation produit quatre effets:
3.1.2.7 Superfacettes : simplification de mailles triangulaires avec une erreur bornée
Cet algorithme [Kalvin & Taylor 1994] de subdivision
adaptative fonctionne très rapidement par rapport à d'autres
méthodes qui assurent des tolérances et des erreurs relatives
à la maille originale limitées. Les sommets résultants
de la simplification forment un sous-ensemble des sommets qui constituent
le modèle original. L'utilisateur spécifie une limite pour
la distance-erreur et l'algorithme assure que la distance entre n'importe
quel sommet de la maille simplifiée et le sommet correspondant de
la maille originale, est inférieure à la limite (Figure
11).
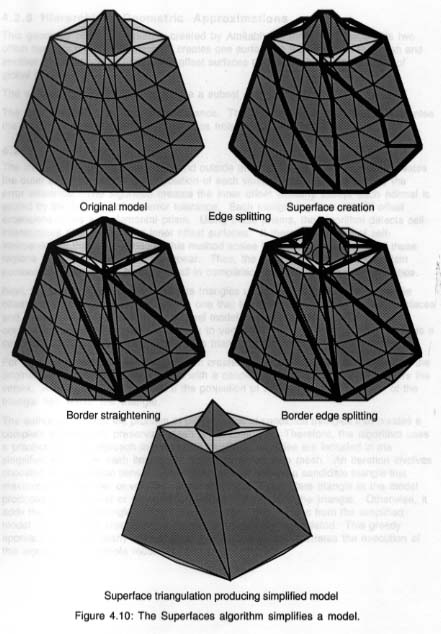
Figure 11 : Algorithme de superfacettes simplifiant un
modèle
3.1.2.8 Approximations géométriques hiérarchisées
Cet algorithme [Varshney 1994] de suppression
géométrique génère deux surfaces d'offset pour
une maille originale (Figure 12). Il s'agit d'une surface
extérieure et d'une autre intérieure à la maille pour
assurer une conservation de la topologie globale. Les sommets résultants
de la simplification forment un sous-ensemble des sommets qui constituent
le modèle original. L'utilisateur définit une tolérance
et l'algorithme utilise cette valeur pour assurer que le modèle
simplifié se trouve au plus à cette distance du modèle
original.
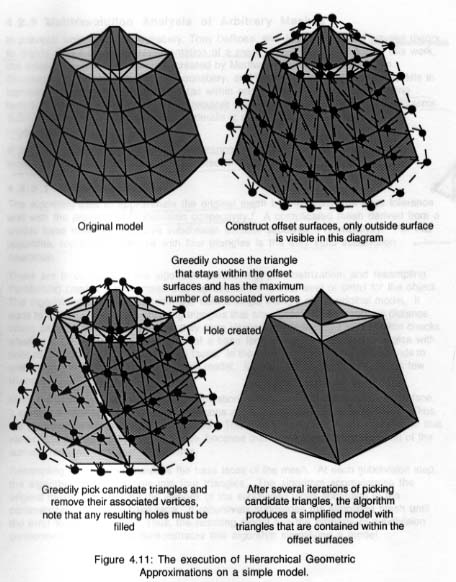
Figure 12 : Application des approximations géométriques
hiérarchisées
3.1.2.9 Analyse multirésolution de mailles arbitraires
Cet algorithme [Eck et al. 1995] [Lounsbery
et al. 1994] de subdivision adaptative utilise la théorie
des ondelettes pour stocker de multiples niveaux de détail dans
un modèle (Figure
Figure 13 9): il s'agit
de réaliser une approximation de la maille originale sans dépasser
une tolérance et en conservant une " connectivité ". Cette
" connectivité " est assurée par l'application d'une règle
d'or : la seule subdivision possible est de remplacer un triangle par quatre
autres en conservant les trois sommets du départ). Une interpolation
entre ces différents niveaux de détail ne demande alors qu'une
addition ou une soustraction de certains coefficients d'ondelette. Si l'utilisateur
spécifie une tolérance à l'erreur en distance, l'algorithme
utilise alors le nombre adéquat de coefficients d'ondelette.
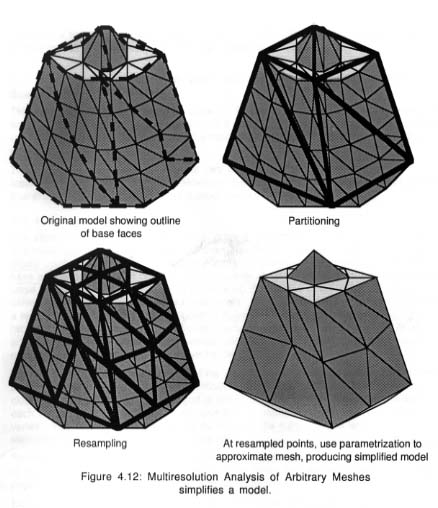
Figure 13 : Simplification d'un modèle a partir
de l'analyse multirésolution
3.1.3 Algorithmes de simplification de la topologie
Les algorithmes qui réalisent une simplification de la topologie ne peuvent pas assurer la conservation de la géométrie locale ou globale du modèle. C'est pour cela que des trous présents sur le modèle original disparaissent pendant l'exécution de l'algorithme. Par contre, ces algorithmes ont un nombre de contraintes plus réduit que les algorithmes qui assurent une conservation de la topologie et par conséquent réalisent une plus grande simplification du modèle.
Ces algorithmes s'utilisent quand une dégradation sensible de
la qualité visuelle est tolérée, souvent en quête
d'une plus grande vitesse de rafraîchissement (frame rate).
Ils sont aussi utilisés quand les autres algorithmes ne fonctionnent
pas.
3.1.3.1 Approximations multirésolution pour le rendu de scènes complexes
Cet algorithme [Rossignac & Borrel 1992] d'échantillonnage fonctionne sur n'importe quel modèle tridimensionnel. Il s'agit d'un choix bien plus intéressant quand on se retrouve face à de grandes scènes qui comportent un nombre élevé de polygones mais qui ne constituent pas des mailles à structure régulière.
Initialement, l'algorithme (Fig Figure 14 ure 10) effectue un classement de tous les sommets du modèle original suivant deux critères:
L'efficacité et la vitesse de cet algorithme se fait au détriment
de l'aspect visuel du résultat puisqu'il n'est pas contraint de
respecter la topologie du modèle originel.
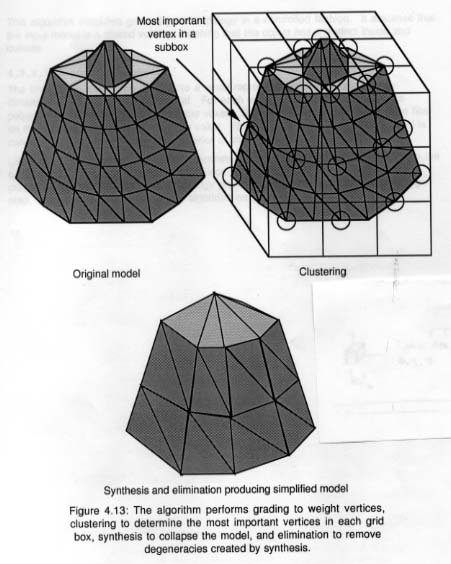
Figure 14 : L'algorithme ne conserve que les sommets
ayant les plus grands coefficients
3.1.3.2 Simplification d?objets axée sur une représentation de voxels
Cet algorithme [He et al. 1995] d'échantillonnage utilise l'approche du traitement du signal et nécessite de solides bases théoriques. Il élimine les détails de haute fréquence du modèle mais il rencontre des problèmes face aux discontinuités abruptes. Cet algorithme effectue une simplification géométrique et topologique " contrôlée ". Il considère le modèle source comme un modèle " fermé ", c'est à dire, que l'objet présente un intérieur et un extérieur distincts.
Premièrement, l'algorithme (Figure 15) remplace l'objet par sa représentation en voxels (cubes unitaires) : il définit une grille de voxels; ensuite, l'algorithme cherche les polygones du modèle qui se retrouvent dans chaque voxel. Puis, il réalise un filtrage passe-bas pour obtenir une valeur de densité. Cette valeur détermine si le voxel doit être considéré à l'intérieur ou à l'extérieur de l'objet.
En utilisant la technique " Marching Cubes ", un algorithme [Lorensen
& Harvey 1987] reconstruit un modèle polygonal simplifié
à partir de la représentation volumétrique de densités.
Puisque l'algorithme de " Marching Cubes " génère des polygones
redondants, cette méthode réalise un post-traitement (algorithme
de préservation de la topologie) comme complément pour éliminer
les redondances. Plus les voxels du grillage sont petits, plus le résultat
se rapproche du modèle original. Si les voxels sont grands, l'algorithme
réalise une grande simplification.
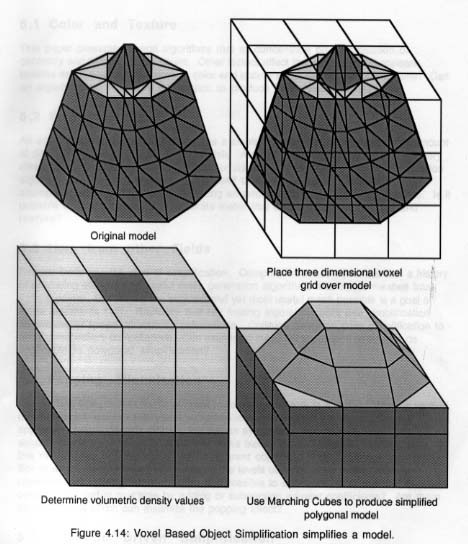
Figure 15 : Simplification du modèle basée
sur la représentation de voxels
Pour la réalisation du projet, ces algorithmes ne seront pas
les plus adéquats puisque il y a une volonté de conserver
le plus grand nombre de détails et de rester fidèle au travail
mené par les chercheurs de la Maison de la Recherche en Sciences
Humaines de l'Université de Caen - Basse Normandie.
3.2 Choix de la méthode
de décimation et réalisation
3.2.1 L'algorithme de suppression géométrique
Le prototype de ce projet met en oeuvre un algorithme de suppression géométrique. Cet algorithme partira du modèle original et réalise une élimination de sommets et de facettes suivant les spécifications de l'utilisateur de façon à réduire la complexité du fichier, mesurée en nombre de polygones.
Le prototype ne correspond exactement à aucune des méthodes
passées en revue. Cependant, la méthode de décimation
développée pour ce projet se retrouve à la base de
certains algorithmes de suppression géométrique [Cohen
et al. 1997] [Cohen et al. 1998]. Elle vise à
mettre en place une première décimation aveugle sur des modèles
géométriques basés sur des ensembles de facettes polygonales
indexées.
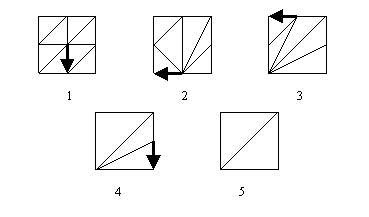
Figure 16 : Application idéale de la méthode
" edge-collapse "
La simplification de mailles de polygones s'effectue suivant la méthode d'élimination d'arêtes (" edge-collapse "). Cette méthode (Figure 16) choisit une arête d'un triangle et ramène un des deux sommets sur l'autre, ainsi l'arête est éliminée. La disparition de l'arête constitue un premier pas de décimation de la maille en un ou deux polygones : un seul s'il n'y a qu'un seul triangle dans l'IndexedFaceSet contenant l'arête en question, ou deux, maximum de triangles ayant la même arête en commun.
Sur la figure 16 on peut voir l'application idéale
de la méthode qui produit une réduction de 6 polygones entre
le modèle n°1 et le modèle n°5.
3.2.2 Décimation aveugle paramétrique
Le prototype programmé en Java (langage choisi pour sa caractéristique multiplateforme) applique fidèlement la philosophie de décimation décrite pour chacun des ensembles de facettes polygonales indexées. Les phases principales de l'exécution sont au nombre de trois : extraction et transtypage des données d'intérêt, décimation de l'ensemble de facettes polygonales indexées et reconstruction du fichier code.
Le processus est le suivant : le prototype lit le code, et le copie
sur le fichier décimé jusqu'à ce qu'il trouve la structure
IndexedFaceSet.
À ce moment là, il arrête la copie, transforme les
chaînes ASCII en types entiers, et enregistre les données
à traiter, puis effectue la décimation. Ensuite, il copie
sur le fichier décimé le résultat du traitement et
continue la copie jusqu'à rencontrer une nouvelle structure IndexedFaceSet.
3.2.2.1 Extraction des données
Dans cette première phase, le prototype fonctionne en mode " parser " : le fichier code VRML est un fichier ASCII. Il est donc nécessaire pour effectuer la décimation d'extraire toute l'information correspondant à l'IndexedFaceSet (non seulement la définition des facettes mais aussi la liste des points constituant le squelette de l'objet). Le prototype réalise une lecture ligne à ligne du fichier source (représentant le modèle à décimer) jusqu'à la totale détection de la structure IndexedFaceSet (Coordinate3 + IndexedFaceSet). à partir de cet instant, le prototype stocke les données dans deux structures vector.
Le vector [Niemeyer & Peck 1997] [Flanagan 1997] est une classe d?ensembles faisant partie de la bibliothèque util de Java. Il s'agit d'un tableau dynamique (il augmente automatiquement sa taille pour accepter de nouveaux éléments) qui gère ses éléments de manière ordonnée. Il permet l'insertion et la suppression des éléments à des endroits arbitraires puisqu'il réorganise ses éléments après chaque modification. Il réalise donc de façon autonome une partie du travail nécessaire avec d'autres langages. Le choix du langage Java est aussi orienté à concevoir un prototype multiplateforme indépendant de la machine sur laquelle il va être exécuté.
La phase d'extraction des données rend deux vector : sommets
et triangles. sommets contient l'ensemble des points constituant
le squelette de l'IndexedFaceSet. triangles représente
la définition des facettes de l'objet : chacun de ses éléments
contient la description d'une facette.
3.2.2.2 Traitement des IndexedFaceSet
L'algorithme de décimation met en place la méthode de
l'élimination d'arêtes (" edge-collapse ") : le prototype
parcourt de façon séquentielle la liste des facettes selon
un pas fixé par l'utilisateur. à chaque pas, l'algorithme
lit la facette et élimine une arête.
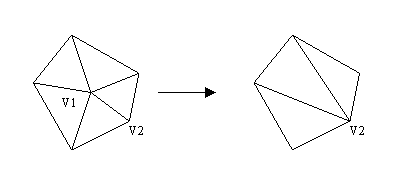
Figure 17 : " Edge collapse ", V1 fusionne sur V2
Comme on peut apprécier sur la figure 17 , l'" edge-collapse " élimine un point (V1) ce qui entraîne la disparition de deux facettes.
Pour une structure donnée, du point de vue du prototype, à
chaque itération l?algorithme choisit une arête (V1,V2) et
réalise les étapes suivantes :
La décimation de l'IndexedFaceSet exige une manipulation
rigoureuse des indices associés au vector car le travail
réalisé automatiquement par Java peut constituer un inconvénient
(erreur différée). En effet, les mises à jour
qui sont effectuées sur les pointeurs du vector doivent être
reportées sur les pointeurs externes employés par l'algorithme.
3.2.2.3 Reconstruction du fichier code
Une fois que l'algorithme finit le traitement de l'IndexedFaceSet,
on dispose des deux vector (sommets et triangles)
et il suffit de les copier sur le fichier décimé. La copie
doit être réalisée cependant en vérifiant le
respect de la structure du fichier original et des règles de composition
du langage VRML.