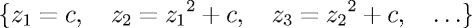
Komplexitet dyker ibland upp p� ov�ntade st�llen. Om vi f�r ett komplext tal c bildar den enkla f�ljden
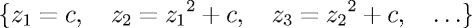
s� visar det sig att vi f�r vissa v�rden p� c f�r en f�ljd vars absolutbelopp snabbt v�xer mot o�ndligheten, medan andra v�rden p� c ger en begr�nsad f�ljd. Detta i sig �r inte konstigt, men det �r f�rv�nande hur sm� variationer i c ger upphov till stora variationer i f�ljdens tillv�xt (man kunde tro att v�rden p� c som l�g n�ra varandra borde ge ungef�r samma resultat, men extremt sm� skillnader kan ge helt olika tillv�xt).
Om vi i det komplexa talplanet markerar de punkter f�r vilka f�ljden �r begr�nsad med en svart prick, och markerar �vriga punkter i en gr�skala som visar hur snabbt de divergerar (exempelvis hur m�nga termer vi m�ste best�mma innan absolutbeloppet �verstiger 2), s� f�r vi f�ljande figur (f�nstrets mittpunkt �r det komplexa talet -0.5 + 0 i, och nedre v�nstra h�rnet �r -1.5 - i):

Redan i denna skala �r figuren intrikat, men om vi zoomar in lite l�ngre, och tittar p� exempelvis omr�det kring 0.282 + 0.01 i s� f�r vi ett �n mer komplicerat utseende (f�rstoringen i denna figur �r 729*729 g�nger st�rre �n i f�reg�ende figur, dvs hela f�nstret motsvarar mindre �n en punkt i f�reg�ende figur):

De punkter som �r svartmarkerade i figuren, allts� de f�r vilka f�ljden �r begr�nsad, tillh�r den s� kallade Mandelbrotm�ngden. Kanten p� m�ngden �r en fraktal, dvs den �r s� 'taggig' att den har en dimension som �r st�rre �n 1, men mindre �n 2 (�ven kristallen i inl�mningsuppgift 4 hade fraktal dimension).
Om vi ist�llet f�r gr�skalor anv�nder olika f�rger (se nedan) kan vi rita figuren ovan som:
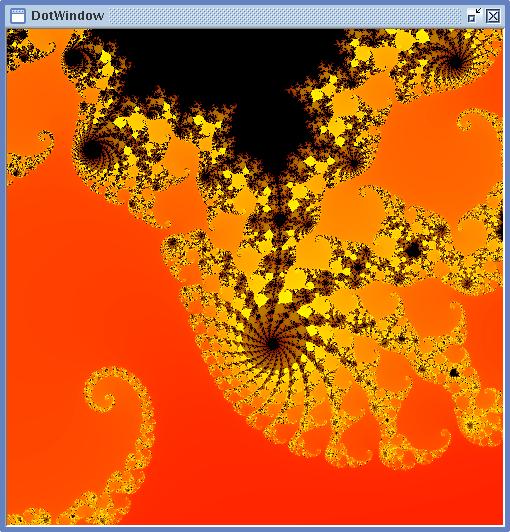
Skriv ett program som visar Mandelbrotm�ngden i ett
DotWindow.
Programmet skall l�ta anv�ndaren zooma in i olika delar av m�ngden genom att klicka med musen, och trycka p� tangentbordet. Exempelvis kan programmet centrera den punkt anv�ndaren klickar p�, och zomma in eller ut om anv�ndaren trycker p� '+' eller '-'-knapparna (den som vill f�r g�rna l�ta anv�ndaren zooma in genom att dra (dvs trycka ner och sl�pa) musen �ver ett omr�de).
Varje punkt i ditt DotWindow motsvarar en punkt i det
komplexa talplanet, programmet skall ber�kna talf�ljden ovan f�r alla
punkter, och markera om f�ljden g�r mot o�ndligheten eller inte genom
att s�tta punkten till en l�mplig f�rg.
Vi kommer r�kna p� talf�ljden i v�ldigt m�nga punkter, och det �r viktigt att det g�r fort, s� vi kan tyv�rr inte anv�nda den klass f�r komplexa tal som vi skrivit tidigare. Ist�llet kan vi skriva en operation:
int calculate(double re, double im)
som ber�knar f�ljden f�r ett komplext tal med realdelen
rm och imagin�rdelen im. I ber�kningen skall
vi addera nya termer tills:
vi uppt�cker att f�ljden g�r mot o�ndligheten (s� snart absolutbeloppet av termerna �verskrider 2 vet vi att den kommer att g� mot o�ndligheten), eller
Operationen calculate skall returnera antalet termer
vi m�ste ber�kna innan vi avbryter, oavsett om vi bryter f�r att
f�ljden divergerar eller f�r att den verkar vara begr�nsad (dvs vi har
ber�knat maximalt antal termer). Detta heltalsv�rde kan vi sedan
anv�nda f�r att best�mma vilken f�rg vi skall rita den aktuella
punkten i. L�mpligt �r att l�ta de punkter som tillh�r
Mandelbrotm�ngden, dvs de i vilka vi ber�knar maximalt antal termer,
vara svarta.
Om vi skall rita i svartvitt kan vi anv�nda gr�skalor (klassen
Grayscale), i linj�r skala fr�n 255 (f�r punkter som
divergerar i ett steg) till 0 (f�r punkter som tillh�r m�ngden). Att
v�lja fler f�rger kr�ver lite experimenterande, i f�rgfiguren ovan har
jag satt maximalt antal iterationer till 255, och d�refter l�tit de
f�rsta 127 f�rgerna g� i en skala fr�n klarr�tt (255,0,0) till
klargult (255,255,0), och d�refter f�rgerna fr�n 128 till 254 i en
skala fr�n klargult till m�rkt r�tt (127,0,0) -- f�rg 255 (dvs sj�lva
Mandelbrotm�ngden) har jag satt till svart.
Programmet m�ste fungera enligt beskrivningen och exemplet ovan. Det r�cker utm�rkt att du kan rita i gr�skalor (du beh�ver allts� inte anv�nda f�rger).
Ditt huvudprogram m�ste brytas ner i underprogram p� l�mpligt s�tt (se tipsen nedan).
Programmet m�ste vara skrivet enligt Javas kodkonventioner, dvs alla indragningar och klamrar skall vara r�tt placerade, och variabler och klasser ha r�ttskrivna namn (exempelvis tydliga namn, liten begynnelsebokstav f�r variabler, stor begynnelsebokstav f�r klasser, etc). Se h�r f�r en kort sammanst�llning av reglerna.
Du f�r sj�lv best�mma vilka klasser du skall ha i denna uppgift. Exempelvis kan du skriva en huvudprogramsklass med f�ljande uppbyggnad:
Globala variabler f�r:
Aktuellt f�nster (DotWindow), l�t g�rna
punkterna vara riktigt sm� -- i exemplen ovan �r
punkterna 1 pixel stora.
F�nstrets storlek (i pixlar) -- vi kan f�ruts�tta att f�nstret �r kvadratiskt.
Aktuell mittpunkt, dvs vilket komplext tal som ligger mitt i f�nstret (real- och imagin�rdel).
F�nstrets skala (i reella tal), dvs hur stor del av reella (och imagin�ra) axeln som syns i f�nstret.
Maximalt antal termer som skall ber�knas i
calculate.
En vektor med vilken f�rg som skall ritas beroende p�
hur m�nga steg calculate beh�vde.
I den f�rsta figuren ovan �r f�nstret 500 pixlar brett och h�gt, mittpunkten (-0.5, 0 i) och f�nstrets skala 2.0 (dvs vi ser reella axeln fr�n -1.5 till 0.5, och imagin�ra axeln fr�n -1 till 1).
Underprogram:
En procedur som s�tter mittpunkten till (-0.5, 0 i), och f�nstrets skala till 2.0. H�r kan vi �ven ge vektorn med f�rger l�mpligt startv�rde.
Funktionen calculate, som beskrevs ovan.
En funktion display, som ritar ut
figuren. Denna operation g�r igenom varje punkt i hela
f�nstret, best�mmer vilket komplext tal den motsvarar,
och anropar calculate.
En huvudloop, som upprepade g�nger anropar
display, och v�ntar p� vad anv�ndaren vill
g�ra.
Olika hj�lpfunktioner f�r att best�mma vilken real- och imagin�rdel en given punkt motsvarar, etc.
Alternativt kan du skriva en Mandelbrot-klass med
attribut motsvarande de globala variablerna ovan, och operationer f�r
underprogrammen. I huvudprogrammet kan du i s� fall skapa ett
Mandelbrot-objekt, och anropa en l�mplig operation f�r
att starta programmet.