Life-spelet

"Spelet" Life uppfanns av den engelske matematikern John Conway i slutet av 1960-talet, och spreds snabbt över världen efter att det omtalats i en artikel av Martin Gardner i Scientific American. Det är egentligen inget spel i vanlig mening, utan snarast en simulering av hur ett samhälle med primitiva organismer kan tänkas utveckla sig.

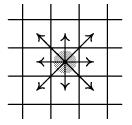
Simuleringen utspelar sig i ett rutnät, där varje ruta (cell) kan vara tom, eller innehålla en levande organism -- varje ruta har 8 grannar (4 vinkelrätt och 4 diagonalt).

Vid simuleringens början läggs levande organismer i ett antal av rutorna, och därefter utvecklar sig livet på spelplanen i ett antal generationer enligt följande regler:

En levande organism överlever om det finns levande organismer i två eller tre grann-rutor.
En levande organism som har mindre än två levande organismer i grannrutorna dör av isolation.
En levande organism som har mer än tre levande organismer i grannrutorna dör av överbefolkning.
I en cell som gränsar till exakt tre rutor med levande organismer föds en ny levande organism.

Alla regler appliceras samtidigt över hela spelplanen, dvs att det föds en ny levande organism i en ruta påverkar inte grannrutorna förrän tidigast nästa generation (samma gäller om en levande organism skulle dö). Om vi skulle börja ändra i spelplanen medan vi beräknar nästa generation kommer de ännu icke behandlade rutor som angränsar till nyfödda organismer att få för många grannar, medan icke behandlade rutor som angränsar till döende organismer skulle få för få grannar. I figuren nedan skapas liv i rutan markerad med 1 (eftersom precis tre grannar, 2, 4 och 5, innehåller levande organismer) -- om vi räknar denna ruta som levande när vi ser vad som skall hända med rutan markerad med 2 så skulle denna dö av överbefolkning (eftersom vi nu förutom grannarna markerade 3, 4 och 5 även har en granne i 1) -- på motsvarande sätt skulle organismen i rutan markerad med 8 dö av isolation om vi redan hade plockat bort organismen i rutan markerad med 5 (som dör av överbefolkning).

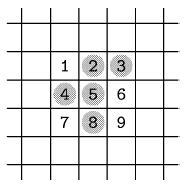
Reglerna kan verka godtyckliga, men är väldigt noga valda för att göra simuleringen så intressant som möjligt.

Uppgift

Din uppgift blir att skriva ett program som låter användaren genomföra simuleringen.

När du skall bestämma nästa generation räcker det att du räknar grannarna i det inre av brädet, du behöver inte behandla kantrutorna (det kan vara lite besvärligt att räkna cirkulärt, runt kanterna - om du ändå skulle vilja göra spelplanen cirkulär så kan du ha stor nytta av operationen mod i klassen CSMath, som hör till kurspaketet).

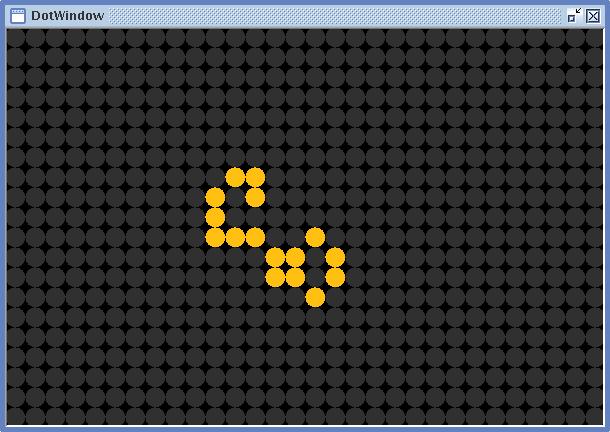
Med kvadratiska prickar i vårt DotWindow hade det varit omöjligt att urskilja de enskilda prickarna i ett större enfärgat område, för att man skall se de enskilda cellerna (rutorna) i fönstret kan det därför vara lämpligt att använda möjligheten att rita runda prickar i ett DotWindow -- figuren nedan visar ett DotWindow med svart bakgrund, och gråa och gulaktiga prickar. Fönstret har 30 prickars bredd, 20 prickars höjd och prickar som har storleken 20 pixlar.

Hur man gör för att rita cirkulära prickar i ett DotWindow beskrivs i dokumentationen av kurspaketet.

Krav för godkänt

Programmet måste fungera. Testa åtminstone de tre konfigurationerna i figuren nedan.
Ditt huvudprogram får inte vara mer än högst några rader långt, det bör anropa underprogram och/eller operationer på lämpliga objekt.
Programmet måste vara skrivet enligt Javas kodkonventioner, dvs alla indragningar och klamrar skall vara rätt placerade, och variabler och klasser ha rättskrivna namn (exempelvis tydliga namn, liten begynnelsebokstav för variabler, stor begynnelsebokstav för klasser, etc). Se här för en kort sammanställning av reglerna.

Tips

För att beskriva själva spelplanen kan vi använda en matris, den kan innehålla boolean-värden (eller möjligen int-värden).
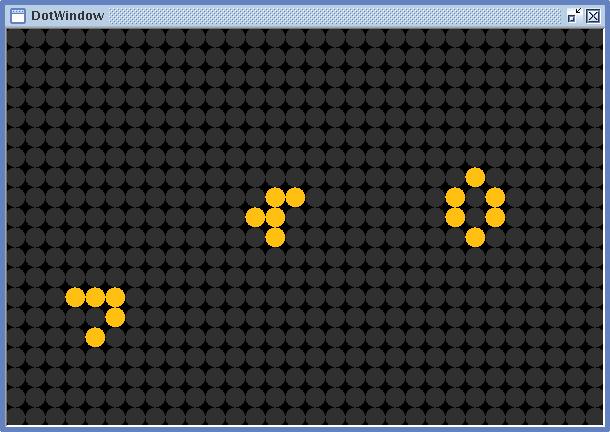
Det finns några konstellationer som du definitivt bör testa, i figuren nedan har vi från vänster till höger
- en "glider", som kommer att glida uppåt åt höger över fönstret (om den inte kolliderar med något annat, vill säga)
- en "R-pentomino", som snabbt ger upphov till förvånansvärt komplicerade mönster
- en "bikupa", som är en av många stabila formationer som ofta uppstår

Några länkar

En sökning på "game of life" ger många 10-tals miljoner träffar på nätet, för den nyfikne kan följande rekommenderas:

Wikipedia.
En kort beskrivning av spelet och några vanliga konfigurationer.
Ett "lexikon" över olika mer eller mindre intressanta formationer. Genom att klicka på formationerna kan du få dem som en vanlig textfil, exempelvis ser filen med en "glider" ut så här:
```
    !Name: glider
    !
    OOO
    O..
    .O.
```
Som ett (naturligtvis frivilligt!) tillägg till ditt program kan du låta användaren ange ett filnamn när programmet startas, och läsa in startformationen från filen. Lägg gärna till en ganska rejäl ram runt figurerna som du läser in, eftersom de förmodligen breder ut sig efter några generationer.