EDAF75 – tentamen i mars 2022, lösningsförslag

Som ofta kan man lösa uppgiften på lite olika sätt, så det är helt OK om ni inte har precis nedanstående modell.

Det finns egentligen inte särskilt många bra naturliga nycklar i modellen, vi skulle kunna designa den så här:

Det är OK om ni skriver ut era 'invented keys', även om det egentligen är en implementationsdetalj:

Det är inte självklart hur vi skall hantera multipliciteten för resurserna, uppgiftstexten sade: "En resurs har ett namn, och en ansvarig karnevalist, och de kan användas vid flera aktiviteter (dock bara en åt gången)". I diagrammen ovan har jag markerat kopplingen mellan Resurs och Aktivitet som en *-* association, men uttrycket "dock bara en åt gången" gör att vi även kan använda en *-1-association.

Valet av vad som skall vara nycklar är ganska fritt, det viktigaste kravet är att det fungerar med lösningarna i (b) och (c).

Det mesta av översättningen från ER-modellen till tabeller klarar vi av med hjälp av några enkla regler:

• Varje entity set (ES) i vår modell kommer att ge en tabell i vår databas:
  • attributen i vår ES kommer att bli kolumner i tabellen
  • om vi har en lämplig naturlig nyckel i vårt ES så kan vi låta den bli primärnyckel i tabellen, annars kan vi introducera en invented key
  • om vår ES har *-1-associationer till andra entity sets (alltså en 1-a på andra sidan), så lägger vi i vår tabell till främmande nycklar som unikt pekar ut ett värde i den andra tabellen (vi gör likadant för alla *-1-associationer från vårt aktuella ES)

• Varje *-*-association ger upphov till en join-tabell, dvs en tabell som kopplar ihop rader i den ena tabellen med rader i den andra tabellen. På en del *-*-associationer har vi associationsklasser, dessa klasser kan bidra med attribut till våra join-tabeller.

  Det är inte ovanligt att studenter använder främmande nycklar på den ena, eller kanske till och med båda sidor i en *-*-association, men det fungerar inte alls, och räknas som ett grovt fel. Om vi har en *-*-association, så får vi en ny tabell.

Vi vill helst ha primärnycklar i samtliga tabeller, och vi bör inte göra dem större än nödvändigt (exempelvis kan vi låta tabellen roller ha nyckeln (stil_id, sektionsnamn), om man bara kan ha en roll i varje sektion – även tupeln (stil_id, sektionsnamn, titel) är naturligtvis unik (den är en superkey), men den är onödigt stor.

För modellen ovan kan vi få (jag har använt stil_id, och förutsatt att samtliga karnevalister har en stil_id, man kan naturligtvis tänka sig andra nycklar, även telefonnummer, även om det inte alltid känns superbeständigt):

CREATE TABLE karnevalister (
  stil_id     TEXT,
  namn        TEXT,
  telefon     TEXT,
  PRIMARY KEY (stil_id)
);

CREATE TABLE sektioner (
  sektionsnamn  TEXT,
  uppdrag       TEXT,
  PRIMARY KEY   (sektionsnamn)
);

CREATE TABLE roller (
  titel         TEXT,
  stil_id       TEXT,
  sektionsnamn  TEXT,
  PRIMARY KEY   (stil_id, sektionsnamn)
  FOREIGN KEY   (stil_id) REFERENCES karnevalister(stil_id),
  FOREIGN KEY   (sektionsnamn) REFERENCES sektioner(sektionsnamn)
);

CREATE TABLE aktiviteter (
  aktivitetsid  TEXT,
  beskrivning   TEXT,
  starttid      DATETIME,
  sluttid       DATETIME,
  PRIMARY KEY   (aktivitetsid)
);

CREATE TABLE uppgifter (
  uppgiftsid    TEXT,
  beskrivning   TEXT,
  aktivitetsid  TEXT,
  stil_id       TEXT,
  sektionsnamn  TEXT,
  PRIMARY KEY   (uppgiftsid),
  FOREIGN KEY   (aktivitetsid) REFERENCES aktiviteter(aktivitetsid),
  FOREIGN KEY   (stil_id) REFERENCES karnevalister(stil_id),
  FOREIGN KEY   (sektionsnamn) REFERENCES sektioner(sektionsnamn)
);

CREATE TABLE resurser (
  resursid     TEXT,
  beskrivning  TEXT,
  stil_id      TEXT,    -- ansvarig
  PRIMARY KEY  (resursid),
  FOREIGN KEY  (stil_id) REFERENCES karnevalister(stil_id)
);

CREATE TABLE resursbokningar (
  aktivitetsid  TEXT,
  resursid      TEXT,
  PRIMARY KEY   (resursid, aktivitetsid),
  FOREIGN KEY   (aktivitetsid) REFERENCES aktiviteter(aktivitetsid),
  FOREIGN KEY   (resursid) REFERENCES resurser(resursid)
);

Ett sätt att rita ER-diagrammet är:

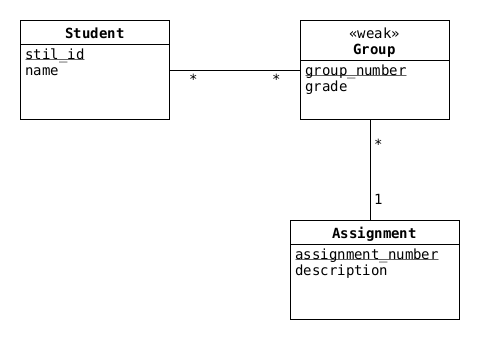
Relationen GroupMembership är egentligen bara en 'join-tabell' för Student och Group, och den finns implicit i vår *-*-association mellan Student och Group, men vi kan rita ut den, antingen som en tom associationsklass på associationen mellan Student och Group, eller som en relation inkilad mellan Student och Group med *-1-relationer till var och en av dem.

I uppgiften ingick inte att definiera tabeller, men vi skulle ha fått något i stil med:

CREATE TABLE students (
  stil_id      TEXT,
  name         TEXT,
  PRIMARY KEY  (stil_id)
);

CREATE TABLE assignments (
  assignment_number  INT,
  description        TEXT,
  PRIMARY KEY        (assignment_number)
);

CREATE TABLE groups (
  assignment_number  INT,
  group_number       INT,
  grade              INT,
  PRIMARY KEY        (assignment_number, group_number),
  FOREIGN KEY        (assignment_number)
                     REFERENCES assignments(assignment_number)
);

CREATE TABLE group_memberships (
  stil_id            TEXT,
  assignment_number  INT,
  group_number       INT,
  PRIMARY KEY        (stil_id, assignment_number),
  FOREIGN KEY        (stil_id)
                     REFERENCES students(stil_id),
  FOREIGN KEY        (assignment_number, group_number)
                     REFERENCES groups(assignment_number, group_number)
);

Lägg in grupp 12 på uppgift 3, och lägg sedan in studenterna med stil-id ’alice’ och ’bob’ i den nya gruppen (du kan förutsätta att både uppgiften och studenterna redan finns i databasen, och att gruppen inte fanns).

INSERT
INTO    groups(assignment_number, group_number, grade)
VALUES  (3, 12, 0);

INSERT
INTO    group_memberships(stil_id, assignment_number, group_number)
VALUES  ('alice', 3, 12),
        ('bob', 3, 12);

Lista uppgiftsbeskrivning och betyg för alla de uppgifter som studenten med stil-id ’alice’ har varit inblandad i (även de ännu inte godkända), ordna efter uppgiftsnummer.

SELECT    description, grade
FROM      assignments
          JOIN groups USING (assignment_number)
          JOIN group_memberships USING (assignment_number, group_number)
WHERE     stil_id = 'alice'
ORDER BY  assignment_number;

Observera att vi testar både assignment_number och group_number när vi joinar in group_memberships, ett sätt att förstå varför vi gör det är följande:

• Vi utgår från tabellen assignments, och har då alltså en rad per uppgift – tabellen ser ut ungefär så här:

  assignment_number  description
  ------------------------------
  1                  Uppgift 1
  2                  Uppgift 2
  ...                ...
  

• Vi vill sedan lägga till information om grupperna för varje uppgift, och joinar därför med groups för att få samtliga projektgrupper för samtliga uppgifter – vi får då \(\sum c_k\) rader, där \(c_k\) är antalet grupper för uppgift \(k\) (om vi antar att vi har \(p\) grupper för var och en av de fyra uppgifterna blir det \(4 p\) rader). Den sammanslagna tabellen ser ut ungefär så här:

  assignment_number  description group_number grade
  -------------------------------------------------
  1                  Uppgift 1   1            3
  1                  Uppgift 1   2            3
  1                  Uppgift 1   3            4
  ...                ...
  2                  Uppgift 2   1            3
  2                  Uppgift 2   2            0
  2                  Uppgift 2   3            5
  ...                ...
  

• Vi vill sedan lägga till information om varje student som är med i varje grupp, så för varje projektgrupp i tabellen ovan vill vi lägga in samtliga deltagande studenter genom att joina in group_memberships. För varje rad i tabellen ovan får vi alltså nu en rad per gruppmedlem – det skulle ge oss en tabell vars rader är ungefär:

  assignment_number  description group_number grade stil_id
  ---------------------------------------------------------
  1                  Uppgift 1   1            3     alice
  1                  Uppgift 1   1            3     bob
  1                  Uppgift 1   2            3     cecilia
  1                  Uppgift 1   2            3     david
  1                  Uppgift 1   3            4     emma
  1                  Uppgift 1   3            4     frank
  ...                ...
  2                  Uppgift 2   1            3     david
  2                  Uppgift 2   1            3     emma
  2                  Uppgift 2   2            3     bob
  2                  Uppgift 2   2            3     alice
  2                  Uppgift 2   3            4     frank
  2                  Uppgift 2   3            4     cecilia
  ...                ...
  

  När vi joinar in stil_id från group_memberships vill vi ju bara få de studenter som ingår i den aktuella gruppen, dvs den grupp vars assignment_number och group_number stämmer överens med raden vi lägger in stil_id på.

Lista stil-id och namn på alla de studenter som är godkända på alla fyra uppgifterna.

Vi kan göra det med en SELECT-sats och en GROUP BY med ett HAVING-villkor:

SELECT    stil_id, name
FROM      students
          JOIN group_memberships USING (stil_id)
          JOIN groups USING (assignment_number, group_number)
WHERE     grade > 0
GROUP BY  stil_id
HAVING    count() = 4;

Alternativt kan vi först bygga upp en tabell med antalet godkända uppgifter för samtliga studenter i en WITH-sats:

WITH pass_count(stil_id, nbr_of_passed) AS (
  SELECT    stil_id, count()
  FROM      students
            JOIN group_memberships USING (stil_id)
            JOIN groups USING (assignment_number, group_number)
  WHERE     grade > 0
  GROUP BY  stil_id
)
SELECT  stil_id, name
FROM    pass_count
        JOIN students USING (stil_id)
WHERE   nbr_of_passed = 4;

Lista stil-id och namn för alla studenter som har det högsta betyg som förekommer på uppgift 1. Det högsta förekommande betyget är inte nödvändigtvis 5 – om du inte kommer på hur man hanterar detta fall det kan du använda betyget 5 istället, men för full poäng vill vi att du bara jämför med det högsta förekommande betyget på uppgiften (du tappar ca 50% om du inte gör det).

Vi kan ta reda på det högsta betyget med hjälp av en subquery, och får då:

SELECT  stil_id, name
FROM    students
        JOIN group_memberships USING (stil_id)
        JOIN groups USING (assignment_number, group_number)
WHERE   assignment_number = 1
        AND grade = (SELECT max(grade)
                     FROM   groups
                     WHERE  assignment_number = 1);

Lista för varje uppgift (alltså 1..4) hur många grupper som ännu inte är godkända (dvs har betyget 0), ordna efter uppgiftsnummer. Vi antar att alla uppgifter och alla grupper är inlagda. Denna deluppgift blir lite knepigare om det finns någon uppgift som alla grupper är godkänd på – för att få poäng på uppgiften behöver du inte hantera detta fall, men för full poäng måste du göra det (du tappar ca 50% om du inte gör det).

Problemet här är att lösningen:

SELECT    assignment_number, count(group_number)
FROM      assignments
          LEFT JOIN groups USING (assignment_number)
WHERE     grade = 0
GROUP BY  assignment_number
ORDER BY  assignment_number;

inte fungerar riktigt som man skulle önska – vår LEFT JOIN ger oss visserligen en rad även för de uppgifter som inte har några grupper kopplade till sig (men alla grupper var inlagda, så det borde inte göra någon skillnad), men när vi sedan testar om grade = 0 så försvinner de uppgifter där alla är godkända, redan innan vi grupperar.

För att få det att fungera kan vi göra en LEFT JOIN (eller, om vi antar att alla grupper är inlagda, en vanlig JOIN) utan att sedan filtrera bort några rader – vi kan göra det med hjälp av en WITH-sats som definerar alla grupper som finns kvar (det finns även andra sätt att lösa det på):

WITH remaining_groups(assignment_number, group_number) AS
  SELECT  assignment_number, group_number
  FROM    groups
  WHERE   grade = 0
)
SELECT    assignment_number, count(group_number)
FROM      assignments
          LEFT JOIN remaining_groups USING (assignment_number)
GROUP BY  assignment_number
ORDER BY  assignment_number;

Vi får följande funktionella beroenden:

• isbn -> title year author classification
• author year -> isbn
• isbn format -> price

Ur dessa kan vi transitivt härleda andra attribut, men det är dessa beroenden som ger poäng (på denna tenta fick man inget avdrag alls om man angav 'härledda' attribut i högerleden av dessa beroenden – det skulle framgå av uppgiftstexten om 'onödiga' extra attribut skulle ge avdrag, normalt gör de det inte).

Vi har alltså:

• R(A,B,C,D,E,F)

och:

• fd1: AB -> E
• fd2: B -> C
• fd3: C -> BD
• fd4: D -> F

Vi kan börja med att ta det transitiva höljet av vart och ett av dessa beroenden:

• fd1: AB -> CDEF
• fd2: B -> CDF
• fd3: C -> BDF
• fd4: D -> F

Vi kan lösa uppgiften utan att bilda dessa transiviva höljen, men att ha beräknat dem minskar risken att missa något transitivt beroende när vi normaliserar nedan (under den sista frågestunden såg vi ett exempel på precis vad som kan hända).

Eftersom A inte förekommer i något högerled måste det ingå i en nyckel, men om vi tar dess transitiva hölje, {A}+, så får vi bara A. Vi måste därför testa alla två-attributkombinationer som innehåller A:

• {AB}+ = ABCDEF
• {AC}+ = ABCDEF
• {AD}+ = ADF
• {AE}+ = AE
• {AF}+ = AF

Här är både AB och AC nycklar, men vi måste även undersöka eventuella tre-attributnycklar – dessa måste innehålla A, men får inte innehålla varken B eller C:

• {ADE}+ = ADEF
• {ADF}+ = ADF
• {AEF}+ = AEF

Så, inga nya nycklar, men vi måste även testa den enda möjliga fyr-attributskombinationen som innehåller A men varken B eller C:

• {ADEF}+ = ADEF

Så, det visar sig att AB och AC är våra enda nycklar.

Vi är inte i BCNF, eftersom vi har funktionella beroenden vars vänsterled inte är supernycklar – detta gäller för fd2, fd3 och fd4 (däremot är fd1 OK, AB är en nyckel).

Hela poängen med normaliseringen är att vi får ett antal tabeller som vi kan join-a ihop igen, till precis samma rader som vi hade från början. Och det är det som är poängen med den metod att normalisera som vi diskuterade under föreläsning 7-8 – att bara skriva upp ett antal relationer som var och en är i BCNF visar inte att vi kan återskapa ursprungstabellen utan förvrängning, så man får inga poäng om man inte följer 'receptet', och det innebär ganska säkert att man blir underkänd på tentan. Så kontrollera noga att du förstår lösningen nedan, och fråga under frågestunder om det är något du är osäker på.

Vi utgår denna gång från:

R(A,B,C,D,E,F)
--------------
fds: AB -> CDEF, B -> CDF, C -> BDF, D -> F
keys: AB, AC

Vi såg ovan att vi inte är i BCNF, och vi kan bryta upp med någon av B -> CDF, C -> BDF eller D -> F (som alla har för 'små' vänsterled) – vi kan välja B -> CDF, och får då dels en relation med attributen i beroendet:

R1(B,C,D,F)
--------------
fds: B -> CDF, C -> BDF, D -> F
keys: B, C

och en relation där vi tar bort de attribut som finns i högerledet i det funktionella beroende vi bröt upp nyss (vi började detta steg med R(A,B,C,D,E,F)):

R2(A,B,E)
--------------
fds: AB -> E
keys: AB

Vi har alltså tagit bort C, D och F här, men behållit B (eftersom det stod i vänsterledet i B -> CDF, och vi därför behöver det för att slå upp C, D och F ur R1).

Här är R2 i BCNF, eftersom dess enda beroende har ett vänsterled som är en supernyckel, men för R1 bryter beroendet D -> F mot BCNF, vi måste därför bryta upp R1 på samma sätt som vi gjorde ovan – först en relation med bara attributen i det funktionella beroendet:

R1a(D,F)
--------------
fds: D -> F
keys: D

och sedan en relation där vi tagit bort attributen i högerledet i beroendet (dvs F, vi kan ju slå upp den ur R1a med hjälp av D) – eftersom vi började detta steg med R1(B,C,D,F) får vi kvar:

R1b(B,C,D)
--------------
fds: B -> CD, C -> BD
keys: B, C

och båda dessa är i BCNF, eftersom samtliga deras funktionella beroenden har vänsterled som är supernycklar.

Vi får alltså:

• R2(A,B,E)
• R1a(D,F)
• R1b(B,C,D)

Om vi i första steget ovan istället bryter upp på C -> BDF eller D -> F så får vi andra relationer, som även de fungerar utmärkt.

För att bygga upp R(A,B,C,D,E,F) från

• R2(A,B,E)
• R1a(D,F)
• R1b(B,C,D)

kan vi joina ihop med hjälp av vänsterleden i de funktionella beroenden som vi använde när vi normaliserade:

SELECT A,B,C,D,E,F
FROM   R1b
       JOIN R1a USING (D)
       JOIN R2 USING (B)

Med andra nedbrytningar (beroende på vilka funktionella beroenden vi bröt upp på), så får vi naturligtvis andra JOIN-satser, men oavsett vilka dessa tabeller och JOIN-satser är, så kommer vi att kunna ta oss tillbaka till ursprungsrelationen utan att förstöra någon information.

Här är ett exempel där vi ursprungligen har en tabell R(A,B,C,D,E,F) med de beroenden vi såg ovan, och följande värden:

A  B  C  D  E  F
-  -  -  -  -  --
1  1  2  3  3  9
1  2  4  5  4  15
2  1  2  3  5  9
2  2  4  5  6  15
3  1  2  3  7  9
3  2  4  5  8  15

Observera att det inte är helt godtyckliga värden – de måste uppfylla de beroenden vi hade.

Med den uppdelning vi gjorde i uppgift 3d ovan kan vi skapa våra nya tabeller som:

CREATE TABLE R1 AS
  SELECT DISTINCT B, C, D, F
  FROM   R;

CREATE TABLE R2 AS
  SELECT DISTINCT A, B, E
  FROM   R;

CREATE TABLE R1a AS
  SELECT DISTINCT D, F
  FROM   R1;

CREATE TABLE R1b AS
  SELECT DISTINCT B, C, D
  FROM   R1;

vilket ger:

---------
R1a:
---------
D  F
-  --
3  9
5  15
---------
R1b:
---------
B  C  D
-  -  -
1  2  3
2  4  5
---------
R2:
---------
A  B  E
-  -  -
1  1  3
1  2  4
2  1  5
2  2  6
3  1  7
3  2  8

Och om vi nu kör

SELECT A,B,C,D,E,F
FROM   R1b
       JOIN R1a USING (D)
       JOIN R2 USING (B)

så får vi:

A  B  C  D  E  F
-  -  -  -  -  --
1  1  2  3  3  9
1  2  4  5  4  15
2  1  2  3  5  9
2  2  4  5  6  15
3  1  2  3  7  9
3  2  4  5  8  15

vilket alltså är precis samma värden som vi startade med.

Två goda anledningar är:

• Vi får färre joins
• Vi kan behålla alla funktionella beroenden (med hjälp av 'constraints' på våra tabeller) – när vi bryter ner hela vägen till BCNF kan några funktionella beroenden 'försvinna' på vägen (se exemplet med bioföreställningarna på föreläsning 8).

De fyra bokstäverna betyder:

• Atomicity: vi vill att ändringar antingen genomförs helt, eller inte alls – vi kan göra en rollback i en transaktion om vi vill återställa ändringar som vi inte vill göra.
• Consistenty: gör att databasen alltid tas från ett korrekt tillstånd till ett annat korrekt tillstånd – vi får denna effekt av våra transaktioner, men egentligen tack vare atomicitet, isolation och durability, så C-et i ACID är egentligen bara en bieffekt av A, I och D.
• Isolation: gör att vi kan köra våra uppdateringar isolerat, som om ingen annan hade tillgång till databasen – detta hanteras helt av transaktioner (och graden av isolering kan ställas in – vid SERIALIZABLE får vi fullständig isolation).
• Durability: garanterar att en ändring kommer att finnas kvar i systemet när vår transaktion väl blivit 'committed'.