Projet Ulysse sur le monde virtuel

Sujet:

Le sujet consiste à réaliser de nouvelles fonctions en prolog de manière à gonfler les fonctions déjà existante. Ces fonctions permettent de naviguer dans un monde virtuel à partir de commande que l'utilisateur saisie. Par exemple, on peut taper avancer, reculer, tourner à gauche, monter, etc ... . Suivant cette saisie, nous voyons dans un monde virtuel avec des objets obéir aux commandes.

Analyse des verbes

Première analyse réalisées:

Pour le choix de verbes:

contourner:

sauter:

regarder:

Analyse plus précise:

Pour réaliser cette analyse plus précise, je vais uniquement prendre le verbe sauter. Après les conseils de Bernard Victorri, nous avons décider de ne plus étudier le verbe regarder. Concernant le verbe sauter, j'ai décidé de me focaliser sur l'expression sauter par dessus. Il est utile de remarquer que cette expression n'est pas dans les différentes définitions données dans les dictionnaires que je possède ("Le Robert Méthodique", "Larousse"). Donc, malgré cette remarque, je vais tenté de donner des définitions.

Etude de termes:

Sauter par dessus :

Le professeur demande à ses élèves de sauter par dessus les haies.
Saute-mouton est un jeu où l'on doit sauter par dessus un autre joueur, qui se tient courbé.
Jacques a du sauter par dessus la chaise pour récupérer le pot de fleurs.

Schéma syntaxique:

N1 + V + prep + N2

avec N2 un obstacle ou un nom de lieu et prep: par dessus

Schéma prédicatif:

SAUTER(loc(y))(x)

Signification:

x fait un saut par dessus y

Commentaire:

Pour ce terme sauter par dessus, nous devons préciser qu'il faut la présence d'un obstacle pour pouvoir effectuer un saut. De plus, le point de départ d'un saut ne nécéssite le besoin d'être au même niveau que le point d'arrivée. Cela signifie que pour le départ nous pouvons être en altitude sur un autre objet. Par contre, le point d'arrivée sera toujours un point au niveau du sol de la cas que nous allons tenter d'implémenter.

D'autres interprétations du terme pourraient poser problème:

Si nous supposons que le point de départ est une table et que le point d'arrivée est une autre table espacée de la première par une distance x. Rien n'empêche de lancer la commande: saute par dessus le vide. Certes c'est un peu tiré par les cheveux, mais c'est fort possible.

Supposons maintenant que nous sommes sur une surface élevée très grande comme une estrade. Sur cette estrade, il y a un cube. Nous pouvons très bien demander à une personne sur cette estrade de sauter par dessus le cube. Dans ce cas, le point d'arrivée, n'est pas au niveau du sol, mais au niveau de l'estrade.

Sauter à droite (à gauche) :

L'entraîneur dit à ses joueurs de sauter à gauche, puis sauter à droite.

Schéma syntaxique:

N1 + V + adv

adv: à gauche, à droite

Schéma prédicatif:

SAUTER(x)

Signification:

x fait un saut vers la droite ou la gauche

Commentaire:

Ce terme de sauter à gauche ou à droite ne pose par de problème particulier. La seule discussion possible concerne la manière par laquelle s'effectue le saut. En effet, 2 cas sont possibles. Le premier cas (celui que nous interpréterons) consiste à effectuer un saut vers la droite sans modification de la direction de la caméra. Dans le deuxième cas, il est possible de se tourner dans la direction du point d'arrivée et de sauter vers l'avant.

Analyse du programme

Après l'analyse des termes que nous venons de faire, la priorité d'implémentation est de réaliser le verbe : sauter par dessus. Pour effectuer un saut par dessus un obstacle, il faut certains pré-requis. Voyons quelques uns de ces pré-requis:

Pré-requis:

La première chose nécessaire est de disposer des coordonnées dans le monde des obstacles. Pour cela, il m'a été nécéssaire d'utiliser la fenêtre d'apprentissage. Celle-ci m'a permis d'avoir des coordonnées relativement correcte pour situer les objets. Je dis relativement correcte, car l'exactitude avec ce procédé n'est pas possible, du fait que nous manipulons nous-même la caméra sous VRML pour nous placer suivant les désirs de la fenêtre d'apprentissage. De plus, une correction des valeurs obtenus est obligatoire pour avoir des données correcctes. Dans le fichier "monde.pl", l'apprentissage commet des erreurs d'écriture, il faut donc les corriger.

Il faut ajouter le verbe sauter et la préposition par dessus dans les fichiers "analyse.pl" (sauter) et "dico.pl" (sauter et par dessus). Pour sauter, nous allons ajouter: tensed_verb(sauter) --> [saute]. Et pour par dessus, nous allons ajouter: prep(par_dessus) --> [par_dessus] et multiword(par_dessus) --> [par, dessus]. Dans le fichier "cle.pl", il faut ajouter: prep(par_dessus,par_dessus).

Nous avons également besoin est une nouvelle fonction correction pour la préposition par-dessus, afin de corriger l'endroit où l'on va.

Description d'un saut:

Comment au sens sémantique pouvons nous définir un saut? Au départ, j'étais parti sur l'idée qu'un saut serait représenté sous la forme d'un demi-cercle ou morceau de cercle. Cette idée fut abandonnée après la réunion avec B.Victorri. En effet, de manière à rester le plus réaliste possible, il ne fallait pas considérer le cercle, mais la parabole.

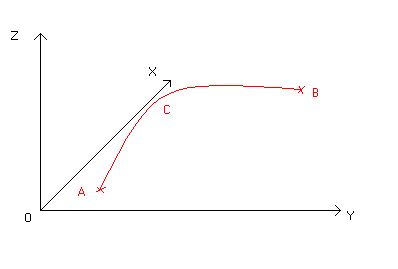
Voyons un exemple de parabole dans un espace 3D: parabole dans espace 3D

Etant donné que nous ne disposons pas sous Prolog de fonctions pour réaliser une parabole, il va falloir rendre cette parabole réaliste dans le cadre du projet. En effet, il n'est pas possible de réaliser la parabole entièrement. Le mouvement de la caméra ne peut pas être direct. De plus, l'utilisation d'une parabole nécéssite l'utilisation de vitesse.
Sur notre schéma, le point A est le point de départ. Le point B est le point d'arrivée. C correspond au sommet de la parabole. Avec la vitesse, nous avons une vitesse décroissante entre A et C. En C, la vitesse est nulle. Entre C et B, la vitesse croît. De cette façon, nous rendons le mouvement de la parabole plus réaliste. Pour réaliser ceci avec les outils que nous disposons, j'ai décidé de découper la distance entre A et B en 10. Ainsi, nous avons 10 temps intermédiaires et 10 vitesses différentes suivant ces temps.

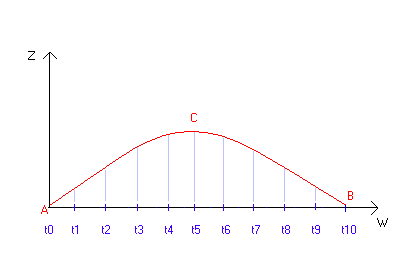
Ce schéma nous montre donc de quelle manière nous allons découper le mouvement de la parabole. Une chose est très importante concernant cet espace en 2D. Nous gardons l'axe de la hauteur avec Z, mais nous créons un nouvel axe avec W. Il est fondamental d'avoir ce nouveau repère pour pouvoir appliquer les formules mathématiques nécessaires à réaliser le calcul de la parbole. Nous remarquons sur ce schéma qu'aux temps t0 à t10, les pentes concernant la parabole varies. Ceci est du à la vitesse que va prendre la caméra au long de sa trajectoire.

Contraintes apportées par un obstacle:

L'apport d'un obstacle pour la parabole va modifier consiérablement les calculs nécéssaires à la réalisation de la parabole. En effet, dans le problème de sauter par dessus un obstacle, les seules données dont nous disposons sont les coordonnées sur l'obstacle. Ceci inclut également la taille de l'objet donné par la fenêtre d'apprentissage. Si nous reprenons le schéma précédent, en incluant un objet à franchier par un saut, nous obtenons le nouveau schéma suivant:

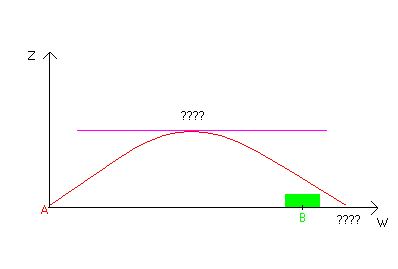
Dans le schéma ci-dessus, nous avons donc un objet représenté en vert. Les seules données dont nous disposons sont les coordonnées du point A et du point B (centre de l'objet). Dans notre calcul de la parabole, il nous faut le sommet et le point d'arrivée. Pour obtenir la point d'arrivée, nous utilisons dans cette première version la taille de l'objet. Sur l'axe W, nous ajoutons 2/3 de la taille de l'objet à la coordonnées W de B. Pour la hauteur, nous considérons 2 fois la taille de l'objet sur l'axe des Z. Ainsi, nous obtenons un coeeficient en fonctions du calcul de la parabole ordinaire. Ce coefficient est utilisé à tous les temps pour obtenir la hauteur de la parabole.

Formules mathématiques résolvant le calcul de la parabole:

Nous avons les formules du calcul de la trajectoire suivantes:

Pour les vitesses:: vw0
Pour les coordonnées des points:: vw0 t + wA

Dans ces formules, t correspond aux temps que nous avons décrits auparavant.